Back ...
... ... ... ... ... ... ... ... ... ... Send comments into the ontology
stream. ... ... ... ... ... ... ... ... ... ... ... Forward
(:….:) … (**) (*) (*) (*) … (:..:)
![]()
Final Report :
Section 1
ARL Contract
TelArt Inc., Chantilly Virginia
December 31, 2000
![]()
In May 2000, Zenkin and
Prueitt discussed the possibility that there might be a common scheme in the
use to CCG technology in new knowledge generation. This discussion occurred
after Dr. Prueitt had developed an appreciation of the Computer Cognitive Graphics
(CCG) technology as it is applied to number theory. Drs Art Murray, Alex
Citkin, Peter Kugler, Bob Shaw, Michael Turvey, and Kevin Johnson have assisted
him in this evaluation. Our first
project report to the ARL delineates this understanding.
Our final report to ARL
generalizes the CCG technology. From the generalized CCG it becomes clear that
the re-application of the original CCG technology to other objects of
investigation can be achieved if and only if all real aspects of the syntactic
and semantic representational problems are addressed.
The claim made in this
ARL Report is that the CCG technology, as applied to number theory, has
addressed all real aspects of the syntactic and semantic representational
problems. A specific object of investigation, this being the theorems of
classical number theory, shapes how these aspects are addressed. No semantic
issues exist, except as noted in the problem of induction. Thus the mass of the
CCG technology is merely formal and syntactic. The core, however, is essential
and this core is about how one manages mental induction.
We hold that induction
is not and cannot be considered algorithmic in nature. We cite Western
Scholarship Robert Rosen and Roger Penrose work as well as the work of J. J.
Gibson and Karl Pribram. Thus the
interface between algorithm computers and human mental activity is necessary in
any generation of new knowledge. It
appears that much of Russian Applied Semiotics is based on this Peircean
concept that an interpretant is actually required during the generation of new
knowledge.
Section 1: A
review of the CCG application to number theory and its generalization
Specifically, elementary
number theory is a formal construct that is built on the Peano axiom, the
additive and multiplicative operators, and on the use of a principle of
mathematical induction. The CCG technology can then be seen to have the
following parts:
A
representational schema
A
visualization schema
An
induction schema
In number theory, the
representation allows color codes to represent division properties. In
classical number theory, division does not induce non-integers, but rather
truth evaluation of whether a remainder is zero, (or any other integer -
depending on the way the theorem is stated). Now it is important to state that
Dr. Prueitt has some background in number theory and as a consequence of seeing
number theory in a new light, there appears to be new theorems regarding
invariances of residues. Perhaps others can see these new theorems also. There
is additional work that would have to be achieved in order to tease a the
specific statement about these theorems.
The possibility of new
mathematics is pointed out only because there is a mental effort required to
think about how color representation fits into the CCG methodology. That this
effort has lead to an intuition about new mathematics is a statement that must
be taken on a plausibility argument. This plausibility is ultimately how the CCG
methodology should be judged. Although
positive results of various types exist and can be shown, the conceptual
grounding for CCG remains foreign, not only due to Russian origin but primarily
due to the misrepresentations made by modern Artificial Intelligence regarding
the nature of human induction.
There is a suggestion
that there are some new theorems that are delineated by Prueitt's mental
intuition when the cognitive effort is made to describe the CCG
techniques. Prueitt is willing to
discuss this issue at the proper time.
However, the existence of new theorems in number theory is not of
immediate interest. Prueitt claims that
the theory of algebraic residues is not completely developed, and that pure
mathematicians who know this field well will be able to quickly see the same
intuition. This intuition comes
immediately from the realization of how color-coding is used in the CCG applied
to number theory.
How would CCG
assist in our experiencing intuitions?
An induction is to be
established by the physical representation (by colors in this case) and the
subsequent representation of truth/falseness evaluation of specific properties
of a generated sequence of numbers using the 2 dimensional grid. Zenkin has
many examples of how this has worked for him. Prueitt sees a different class of
theorems because he has a different mathematical training and internal percepts
about the Peano axiom and the additive and multiplicative operators. Any other
pure mathematician would see theorems that are new, depending on the nature of
the intuitions that are resident in the mind of the pure mathematician. CCG would be useful in the completion of
mathematical reasoning from whatever experience the mathematician might have.
Prueitt holds that any
formal system can be vetted using slight modifications of the CCG
representation and visualization demonstrated by Zenkin. If this claim is
correct, then areas of abstract algebra would fall under the technique. The
requirement is that a human has deep intuitions about an object of
investigation and that the representation and visualization setup a route to
induction regarding truth / falseness of theorems (see the work of Russian
father of quasi axiomatic theory, Victor Finn, on routs to induction).
This means that someone
who is deeply involved with algebra and who studied the CCG applications to
number theory would likely begin to (immediately) see how to represent and
visualize relationships such as the property of being a generator of a semi
group. Once this new mental intuition is established, then a principle of
induction is required that allows the validation, or falsification, of
intuitions. In the past application of CCG to number theory, this validation of
intuition is equivalent to a formal proof, and yet is made using a proxy that
is visual in nature. The proxy is established via the notion of a super-induction
where the visual observation of a property transfers to a formal declaration of
fact. This transfer is the core of the CCG technology and is not dependent on
the specific representation or the visualization, as long as the visualization
schema matches (completely) all syntactic and semantic representational
problems.
In formal systems, the
problem of syntactic and semantic representation is not only simple; but is
also complete. There is little or no semantic dimension. Only the truth
evaluation is semantic and this semantic evaluation is incompletely represented
in the iterated folding of syntactic structure (via rules of deductive
inference). In essence, one can almost claim that the only semantic aspect
about number theory is that someone who sees the elegance of it can experience
it as beautiful. The caveat is captured by the Godel theories on completeness
and consistency, and on related notions communicated by Cantor and others
(including Robert Rosen’s work on category theory). Of course, Zenkin is one of
those who have advanced a disproof of Cantor's argument regarding the
categorical non-correspondence between the whole numbers and the real numbers.
Prueitt reads this
disproof in a certain way. The argument that Canton's diagonalization theory is
flawed is really a comment on the nature of common mathematical induction. As
Kevin Johnson has pointed out, there are many many ways to perform an
induction. The common mathematical induction simply depends on
an ordering of theorems in such a way that the tail of this sequence of
theorems has invariance with respect to the truth evaluation. The CCG representation and visualization simply allows a
pure mathematician a by-pass of all orderings except one that results in
visualization of the targeted invariance of a tail of a sequence of
theorems. This by-pass is
non-algorithmic and thus must be managed by a human.
One can see this as a
search space problem. In many cases modern computer science has identified what
are called NP-complete problems. The NP-complete problem can be proved not to
be computably solved with the iterative application of the folding
(application) of the fundamental axioms and properties in the set up of the
formal system. However, visual acuity by a human might see a route to a
solution. In fact, Prueitt has made the argument that biological systems have
evolved in such a way as to by-pass NP complete problems. He claims that the
capacity for seeing a solution that cannot be computed is fundamental to
biological intelligence.
In formal systems, the by-pass
is simply a lifting away from and a replacement into the formal construct. This
there is still no semantic dimension to the solution. This concept of lifting
is consistent with Brower’s notion of intuition (Bob Shaw – private
communication). This means that the
solution, once found, to NP-complete problems can then be proved using common
inference and common induction. It is just a question of skipping and
reordering.
Possible
application to EEG and stock market data analysis
Zenkin and Prueitt were
hoping that EEG data could be easily found with expert opinions about
differential meaning of data patterns in context. Due to the uncertainty of how
we might precede Prueitt did not pursue a collaborative relationship with EEG
experts in Karl Pribram's lab or in any other lab. Such collaboration requires
that the method we have devised for visualization be well developed and that
our collaborative project with the Russians be well funded.
As we worked on this
issue, it became clear that we could describe such a method only if the
communication between Russia and the United States was better. We need to involve neuroscientists both in
St. Petersburg (Juri Kropotov) and in the USA (Karl Pribram).
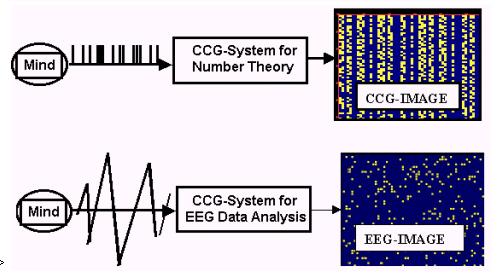
Given our limited
resources, Prueitt decided to attempt to generalize the CCG methodology and
then project this generalization back onto some object of investigation. The
idea was that the generalization and separation of parts of the CCG techniques
would show us how to proceed.
What we needed to figure
out first was how to characterize the CCG method in such a way that aspects of
the method could be separated into functional parts. Then each part might be
generalized and then projected into a new use case.
We were open to possible
investment directed at using indices in the analysis of stock market
performance. This possibility still exists. However, it is felt that this
application is unwise and not directed at a scientific or mathematical
objective.
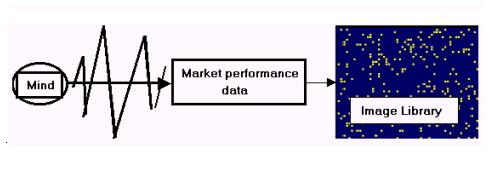
However, our thinking
about the markets allowed us to see, for the first time, that we needed to have
an Image Library. We needed a repository for the consequences of the evocation
of knowledge about, or an intuition about, the past or future performance of
the market. At this point, the work of other Russian applied semioticians
(Pospelov and Finn) come into play. The Library becomes a repository for a system
of tokens, each token deriving token meaning from intuitions vetted by the CCG
representation and visualization, and confirmed by an induction. The system is
then a formalism that is open to human manipulation as well as formal
computations. The formalism has both a first order and a second order (control
or tensor) system.
We have come face to
face with the core difference between a formal system, like number theory or
algebra, and a natural object of investigation, like the stock market. It is
this difference that is ignored by most Western mathematicians and computer
scientists. It is also this difference that illuminates the nature of Russian
applied semiotics. The case of this assertion will not be full made here; as to
some extent the assertion is ultimately a statement of belief.
In any case Zenkin and
Prueitt both agreed that an Image Library might be built as a type of Artifact
Warehouse, where the artifacts were the consequences of a super-induction
mediated by some representational and visualization schema.
The problems are then
defined as
How
does one represent the object of investigation
How
does one visualize the accrual of invariance
How
does one establish conditions of induction
Prueitt has some
experience with scatter gather methods used in the standard methods for
vectorization of text. Thus he chose a collection of 312 Aesop fables to be his
target of investigation. This choice was a secondary choice, since TelArt
Incorporated continued to hope that situations in Russian might allow Alex
Zenkin the time required to make a paper on his own attempted application of
CCG to scientific data of some sort. As the deadline for our Final Report
neared, it became clear that Prueitt would have to write the Final Report
without additional original work from Russia.
In the next sections,
results of the generalization of CCG are applied to the problem of parsing
text. Text parsing ultimately is to be applied to a routing of information or a
retrieval of information. Prueitt is designing a system for a worldwide
evaluating of Indexing Routing and Retrieval (IRR) technologies, and thus the
use of Prueitt's background was capitalized on for the purpose of completing
our contractual obligations.
The URL announcing this
IRR evaluation is at: link